
💫 알고리즘
DP(동적 계획법)
복잡한 문제를 작은 부분 문제로 나누어 해결
그 결과를 저장하여 전체 문제의 최적해를 구하는 알고리즘
중복되는 부분 문제를 반복적으로 해결하면서 최적화된 솔루션을 찾는 접근 방식
💡 풀이방향
🐢 해당 문제는 DP 중 최장 공통 부분 수열(LCS) 문제
1️⃣ LCS 문제는 두 수열이 주어졌을 때, 모두의 부분 수열이 되는 수열 중 가장 긴 것 찾는 문제
2️⃣ 입력으로 두 문자열이 주어짐
A = [""] + list(입력 문자열)와 같이 앞에 빈 문자열 ""을 추가
문자열 A와 B를 1-indexed로 두어, DP 테이블을 구성할 때 인덱스 맞추기 편하도록
3️⃣ dp 테이블 초기화
dp[i][j]는 문자열 B의 i번째 글자, 문자열 A의 j번째 문자 사이의 최장 공통 부분 수열 문자열 의미
4️⃣ 이 문제는 단순히 LCS의 길이만 출력하는 게 아닌 LCS도 출력해야 됨
; 따라서 dp 테이블엔 LCS의 길이를 갱신하는 게 아닌 LCS를 갱신
👀 풀이
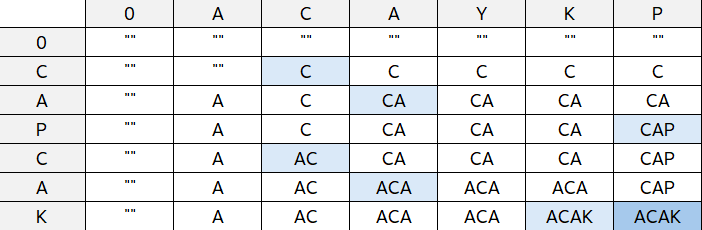
dp 테이블을 시각화하면 위와 같은데요.
dp[i][j]: 문자열 B의 i번째 글자, 문자열 A의 j번째 문자 사이의 최장 공통 부분 수열 문자열
이해를 위해 예시를 들어볼게요!
A[3] == B[2]가 왜 CA ?
이중 반복문을 돌며 ↘ 방향으로 공통 부분 수열이 갱신
---
이전 부분 문제
B의 index = 1인 'C', A의 index = 2인 'C'사이의 최장 공통 부분 수열 문자열은 'C'
현재 B의 index = 2은 'A', A의 index = 3은 'A'로 일치
---
이전 부분 문제의 LCS에 현재 일치한 문자를 추가
B의 index = 2, A의 index = 3사이의 최장 공통 부분 수열 문자열은 'CA'
반복문을 돌면서 현재 B의 index, A의 index 사이의 최장 공통 부분 수열 문자열을 갱신한다고 생각하시면 돼요!
🌟 코드 구현
import sys
input = sys.stdin.readline
A = [""] + list(input().strip())
B = [""] + list(input().strip())
dp = [[""] * len(A) for _ in range(len(B))]
for i in range(1, len(B)):
for j in range(1, len(A)):
if A[j] == B[i]: # 문자가 일치하다면
dp[i][j] = dp[i-1][j-1] + A[j] # 최장 공통 부분 수열 문자열 갱신
else: # 문자가 일치하지 않으면 이전 부분 문제 중 더 긴 문자열로 갱신
if len(dp[i][j-1]) > len(dp[i-1][j]):
dp[i][j] = dp[i][j-1]
else:
dp[i][j] = dp[i-1][j]
LCS_len = len(dp[-1][-1])
print(LCS_len)
if LCS_len != 0:
print(dp[-1][-1]) # LCS'백준' 카테고리의 다른 글
| [백준/Python(파이썬)] 9663 (0) | 2025.02.11 |
|---|---|
| [백준/Python(파이썬)] 2565 (0) | 2025.02.10 |
| [백준/Python(파이썬)] 11054 (0) | 2025.02.09 |
| [백준/Python(파이썬)] 1655 (0) | 2025.02.08 |
| [백준/Python(파이썬)] 12865 (1) | 2025.02.06 |
