https://www.acmicpc.net/problem/11444
골드 2 피보나치 수 6

💫 알고리즘
분할 정복 Divide and Conquer
문제를 더 작은 하위 문제들로 분할
각 하위 문제를 재귀적으로 해결
해결된 하위 문제들을 결합하여 전체 문제의 해답을 도출
💡 풀이방향
🐢 분할 정복(: Fast Doubling을 통해)을 활용한 피보나치 수 계산
1️⃣ 주어진 n에 대해 F(n)을 구하고, 이를 1,000,000,007로 나눈 나머지 구하기
2️⃣ n의 범위가 최대
3️⃣ 피보나치 수의 기본 점화식 F(n) = F(n - 1) + F(n - 2)
4️⃣ Fast Doubling을 이용한 분할 정복

홀수 번째 계산

5️⃣ 모듈러 연산을 통해 큰 수 처리
계산 도중 값이 매우 커질 수 있으므로, 모든 연산에 모듈러 연산(%) 적용
🌟 코드 구현 + 👀 풀이
[전체 코드]
import sys
input = sys.stdin.readline
MOD = 1000000007
# (F(n), F(n+1))을 반환하는 함수
def fib(n):
if n == 0:
return (0, 1)
a, b = fib(n // 2)
c = (a * ((2 * b - a) % MOD)) % MOD # 짝수 번째 계산 F(2k)
d = (a * a + b * b) % MOD # 홀수 번째 계산 F(2k+1)
if n % 2 == 0:
return (c, d)
else:
return (d, (c + d) % MOD) # (c + d): F(n - 1) + F(n - 2)
n = int(input())
print(fib(n)[0])
fib 함수
빠른 피보나치 계산(Fast Doubling)
# (F(n), F(n+1))을 반환하는 함수
def fib(n):
if n == 0:
return (0, 1)
a, b = fib(n // 2)
c = (a * ((2 * b - a) % MOD)) % MOD # 짝수 번째 계산 F(2k)
d = (a * a + b * b) % MOD # 홀수 번째 계산 F(2k+1)
if n % 2 == 0:
return (c, d)
else:
return (d, (c + d) % MOD) # (c + d): F(n - 1) + F(n - 2)if n == 0: return (0, 1)
Base case
n = 0일 때, F(0) = 0, F(1) = 1이므로 (0, 1) 반환
a, b = fib(n // 2)
재귀 호출을 사용, 피보나치 수를 절반으로 줄여 계산
재귀적으로 계산함으로써 O(log n)의 시간 복잡도
c = (a * ((2 * b - a) % MOD)) % MOD
짝수 번째 계산 F(2k)
F(2k) = F(k) * (2F(k + 1) - F(k))
a: F(k), b: F(k + 1)
d = (a * a + b * b) % MOD
홀수 번째 계산 F(2k + 1)
F(2k + 1) = F(k)^2 + F(k + 1)^2
a: F(k), b = F(k + 1)
if n % 2 == 0:
return (c, d)
else:
return (d, (c + d) % MOD) # (c + d): F(2k) + F(2k+1) = F(2k+2)if n % 2 == 0: return (c, d)
짝수인 경우 반환값은 (F(2k), F(2k + 1))
c, d는 각각 F(2k)와 F(2k + 1)
else: return (d, (c + d) % MOD)
홀수인 경우 반환값은 (F(2k + 1), F(2k + 2))
F(2k + 2)는 c + d # F(n) = F(n - 1) + F(n - 2) 생각

📢 더 보기
🐢 점화식을 이용해 다른 방식으로도 풀 수 있어요
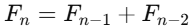
을 행렬 형태로 변환하면


구해야 할 값은 [[1, 1], [1, 0]] 행렬의 n - 1거듭제곱의 첫 번째 행, 열 원소
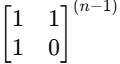
import sys
input = sys.stdin.readline
MOD = 1000000007
# 행렬 곱셈 함수
def multi(X, Y):
global N
C = [[0] * N for _ in range(N)] # 결과 행렬 C 초기화
for i in range(N):
for j in range(N):
for k in range(N):
C[i][j] += X[i][k] * Y[k][j]
C[i][j] %= MOD
return C
# 행렬 거듭제곱 함수
def mat_pow(A, B):
global N
if B == 1:
for i in range(N):
for j in range(N):
A[i][j] %= MOD # 나머지 연산 적용
return A
half = mat_pow(A, B // 2)
if B % 2 == 0:
return multi(half, half)
else:
return multi(multi(half, half), A)
def fibonacci(n):
global N
if n == 1:
return 1
elif n == 0:
return 0
N = 2 # 행렬 크기 설정
base_matrix = [[1, 1], [1, 0]] # 기본 피보나치 행렬
result_matrix = mat_pow(base_matrix, n - 1) # A^(n-1) 계산
return result_matrix[0][0] # F(n) 값 반환
n = int(input())
print(fibonacci(n))
'백준' 카테고리의 다른 글
| [백준/파이썬] 2110 (0) | 2025.02.24 |
|---|---|
| [백준/파이썬] 11401 (0) | 2025.02.23 |
| [백준/파이썬] 10830 (0) | 2025.02.20 |
| [백준/파이썬] 1931 (1) | 2025.02.19 |
| [백준/파이썬] 25682 (0) | 2025.02.18 |
