https://www.acmicpc.net/problem/11401
골드 1 이항 계수 3

💫 알고리즘
분할 정복 Divide and Conquer
문제를 더 작은 하위 문제들로 분할
각 하위 문제를 재귀적으로 해결
해결된 하위 문제들을 결합하여 전체 문제의 해답을 도출
💡 풀이방향
🐢 팩토리얼과 모듈러 역원을 활용한 이항 계수 계산(페르마의 소정리)
1️⃣ 주어진 N과 K에 대한 이항 계수
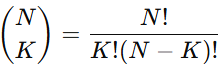
를 1,000,000,007로 나눈 나머지를 구하는 문제
2️⃣ 모든 연산에 mod 연산 수행
N이 최대 4,000,000,0이고, 팩토리얼 연산을 해야 하므로
3️⃣ 페르마의 소정리를 활용해 모듈러 역원 계산
이항 계수 공식에서 분모에 해당하는 K!(N - K)!로 나누어야 하는데,
모듈러 산술에서는 직접 나눗셈 불가
따라서 모듈러 역원을 구하는데, MOD가 소수이므로 페르마의 소정리 적용
페르마의 소정리
a: 정수, p: 소수, a와 p는 서로소

양변에 a의 모듈러 역원 a^(-1)을 곱하면

위를 사용하여 나눗셈을 모듈러 역원으로 나타냄
4️⃣ 위에서 구한 모듈러 역원을 이용해 이항 계수 계산
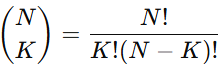
을 N! * ((K! * (N - K)!)^(mod - 2)) (mod MOD)로 계산
🌟 코드 구현 + 👀 풀이
[전체 코드]
import sys
input = sys.stdin.readline
MOD = 1000000007
def fact(num, mod):
n = 1
for i in range(2, num + 1):
n = (n * i) % mod
return n
def inv_fact(base, exp, mod):
if exp == 1:
return base % mod
x = inv_fact(base, exp // 2, mod)
if exp % 2 == 0:
return x * x % mod
else:
return x * x * base % mod
N, K = map(int, input().split())
numerator = fact(N, MOD)
denominator = fact(K, MOD) * fact(N - K, MOD)
print(numerator * inv_fact(denominator, MOD - 2, MOD) % MOD)
팩토리얼 계산 함수 fact(num, mod)
def fact(num, mod):
n = 1
for i in range(2, num + 1):
n = (n * i) % mod
return nn = 1로 초기값 초기화
2부터 num까지 반복
매 반복마다 n에 현재 i를 곱한 후 % mod 연산을 통해 모듈러 연산
모듈러 역원(+ 빠른 거듭제곱) 계산 함수 inv_fact(base, exp, mod)
def inv_fact(base, exp, mod):
if exp == 1:
return base % mod
x = inv_fact(base, exp // 2, mod)
if exp % 2 == 0:
return x * x % mod
else:
return x * x * base % modif exp == 1: return base % mod
base case
x = inv_fact(base, exp // 2, mod)
재귀 호출을 이용, 빠른 거듭 제곱
if exp % 2 == 0: return x * x % mod
짝수인 경우 단순히 제곱
else: return x * x * base % mod
홀수인 경우 * base까지
이항 계수 계산
N, K = map(int, input().split())
numerator = fact(N, MOD)
denominator = fact(K, MOD) * fact(N - K, MOD)
print(numerator * inv_fact(denominator, MOD - 2, MOD) % MOD)numerator = fact(N, MOD)
분자 계산 N! mod MOD
denominator = fact(K, MOD) * fact(N - K, MOD)
분모 계산 K! * (N - K)! (mod MOD)
print(numerator * inv_fact(denominator, MOD - 2, MOD) % MOD)
모듈러 산술에서는 나눗셈 대신 역원을 곱함
inv_fact(denominator, MOD - 2, MOD)을 통해 분모의 모듈러 역원을 계산

'백준' 카테고리의 다른 글
| [백준/파이썬] 11723 (0) | 2025.02.26 |
|---|---|
| [백준/파이썬] 2110 (0) | 2025.02.24 |
| [백준/파이썬] 11444 (0) | 2025.02.22 |
| [백준/파이썬] 10830 (0) | 2025.02.20 |
| [백준/파이썬] 1931 (1) | 2025.02.19 |
